Table of contents
The 0-1 Knapsack is a classical DP problem that is asked in interviews.
Simply put, we are given a set of values and their corresponding weights. We need to determine the items to include in a knapsack so that the sum of those values/weights is the maximum possible. The weight should be less than or equal to the given knapsack weight.
One important thing to note here is that we have two options: to include the weight in the knapsack and or exclude it.
There are three ways to solve a DP Problem i.e. by Recursion, Memoization, and Tabulation. I am going to show all three one by one.
Recursion
In Recursion, we first write the base case. Suppose the given limit/weight of the knapsack is 'W' and 'n' is the number of items/values in the array. Then if W is equal to zero, i.e, if the limit of the knapsack is already zero, then we cannot put any weight into the knapsack and if there are zero items for us to put, then what will we put in the knapsack, therefore it is our base case in recursion.
After that shown below, we use the condition that if the weight of the item is less than or equal to the weight of the knapsack then only we can further proceed. At that time we have two options, either to include or exclude that item so that we can get the maximum result. So recursively we call for 'include' as shown. If we include then we add the value of the item and then call for 'n-1' items. Also if we include the item, and put it in the knapsack, then we are left with 'W-w' weight. For exclude, we just exclude that item and call for the rest of the items. Then we calculate, from which of the two scenarios we get the maximum value, and then we return it. The time complexity of recursion is O(2^n), which is very inefficient.

Memoization
Memoization is a technique used in dynamic programming to optimize the recursive solution of problems by storing the results of expensive function calls and reusing them when needed. It can be applied to the 0-1 Knapsack problem to improve its efficiency. In recursion, we make calls every time for each result, which makes the recursion technique inefficient. So by using memoization and storing results in a dp array, we make the code very efficient with the time complexity of O(n * W). As shown in the code I have stored the calculated result in a DP Array (dp[n][W]). So this way we don't have to calculate each time, instead use the answer which is already stored in the array, which reduces the time complexity.

Tabular method
Simply speaking, tabulation is another technique used in dynamic programming to solve problems iteratively using a table or an array. It avoids recursion and builds up the solution by filling the table from smaller subproblems to larger ones. We use a 2D array to store the answers to smaller subproblems and eventually go to larger ones.
Firstly we initialized the 1st row and column with zero. Then started to fill the matrix with the values and weight of the knapsack given. The answer is stored in the last cell of the 2D array as shown below. Because we have to make the largest profit, so cell by cell each profit is stored. Like for say, (2, 4) i.e we include from 0 to 2 th place in values and 0 to 4 weight how much profit we can make, and that result is stored in (2, 4)th or (i, j)th cell of the matrix. And this way we get to the last cell of the array where we include all values and weights.
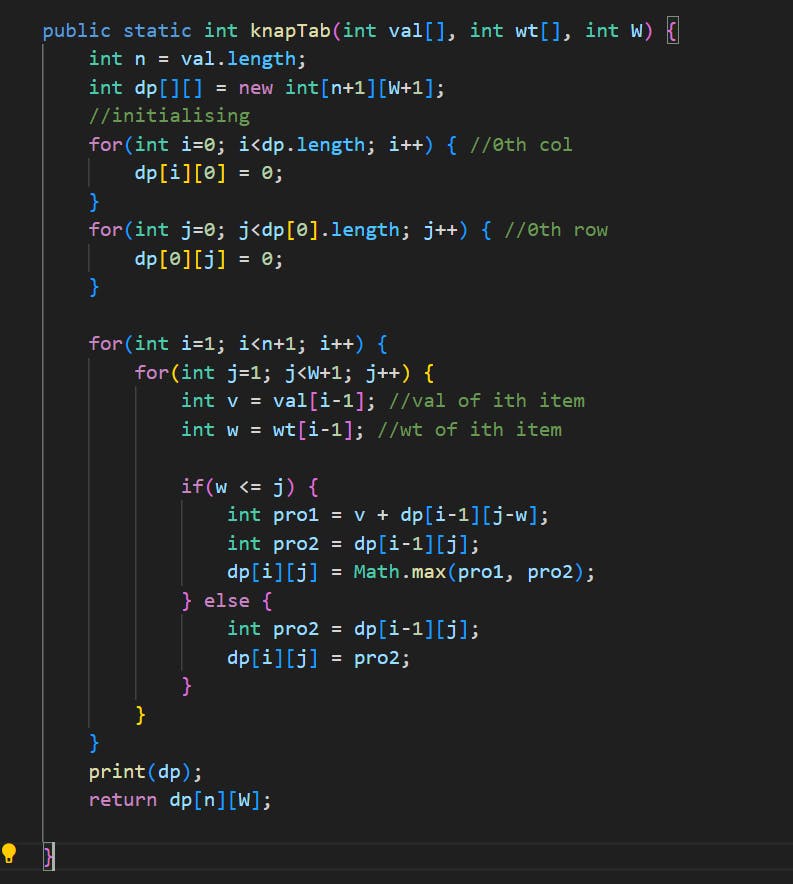
So I have tried to explain the tabulation method in a better way below. It is a very important method in Dynamic Programming and therefore should be understood clearly. The time complexity of the tabulation is O(n * W).

I have tried my best to explain the knapsack problem. Make sure to practice more such problems on coding platforms like leetcode, codeforeces, etc.
Hope it helped :)
